Molecular Vision 2006; 12:949-960 <http://www.molvis.org/molvis/v12/a107/> Received 6 February 2006 | Accepted 21 July 2006 | Published 16 August 2006

Download Reprint

Automated tool for the detection of cell nuclei in digital microscopic images: Application to retinal images

Jiyun Byun,^1,2 Mark R. Verardo,^2,3 Baris Sumengen,^1,2 Geoffrey P. Lewis,^2,3 B. S. Manjunath,^1,2 Steven K. Fisher^2-4
 
 

¹Department of Electrical and Computer Engineering, ²Center for Bio-image Informatics, ³Neuroscience Research Institute, ⁴Department of Molecular, Cellular and Developmental Biology, University of California, Santa Barbara, CA

Correspondence to: Jiyun Byun, Department of Electrical and Computer Engineering, Center for Bio-image Informatics, University of California, Santa Barbara, CA, 93106; Phone: (805) 893 2526; FAX: (805) 893 3262; email: jiyun@ece.ucsb.edu

Abstract

Purpose: To develop an automated tool that provides reliable, consistent, and accurate results for counting cell nuclei in tissue sections.

Methods: We propose a novel method based on an image processing algorithm to analyze large sets of digital micrographs. The nucleus detector design is based on a Laplacian of Gaussian filter. We use the leave-one-out cross validation method for estimating the generalization error, which is then used to choose the model and parameters of the proposed nucleus detector with both fluorescent and dye stained images. We also evaluate the performance of a nucleus detector by comparing the results with manual counts.

Results: When our nucleus detector is applied to previously unanalyzed images of feline retina, it correctly counts nuclei within the outer nuclear layer (ONL) with an average error of 3.67% ranging from 0 to 6.07%, and nuclei within the inner nuclear layer (INL) with an average error of 8.55% ranging from 0 to 13.76%. Our approach accurately identifies the location of cell bodies. Even though we have a relatively large error in the INL due to the large intra-observer variation, both manual counting and nucleus detector result in the same conclusion. This is the first time that cell death in the INL in response to retinal detachment is analyzed quantitatively. We also test the proposed tool with various images and show that it is applicable to a wide range of image types with nuclei varying in size and staining intensity.

Conclusions: The proposed method is simple and reliable. It also has widespread applicability to a variety of sample preparation and imaging methods. Our approach will be immediately useful in quantifying cell number in large sets of digital micrographs and from high-throughput imaging. The tool is available as a plug-in for Image J.

Introduction

Cell addition and loss are important biological events in development and pathology. As a result, counts of cells and nuclei from histological sections provide quantitative information central to studying changes in cells, tissues, and organs. For example, neuron number is a fundamental determinant of brain function [1] and the number of photoreceptors is a common measurement of visual function of retina [2-6]. While progress in understanding changes in such parameters as cell structure or protein expression has been rapid during the past few decades, methods for determining cell number have remained limited. Determining the numerical density of cells in sectioned materials is difficult. Indeed, even the most rigorous studies rarely claim precision greater than ±10% [1]. Consequently, only marked changes or effects can be analyzed with confidence. Several solutions to this problem have been proposed, but they require significant resources in order to complete a morphometric analysis. Moreover, most of these methods still require manual counting, which is tedious and time consuming, regardless of whether a 2-D or a 3-D methodology is employed. In carrying out such work, biologists need to sit for long periods of time performing microscopic sampling and their physical and mental fatigue can impact the speed and quality of information. Problems that demand greater accuracy and reliability cannot be resolved with current manual methods.

Image analysis methods have been developed for nucleus detection or segmentation. In the past, algorithms developed for automatic micrograph analysis have been very task specific and are not easily extensible to analysis of different types of images such as those generated by immunofluorescence. For example, Malpica [7] used a watershed transformation to segment clustered nuclei. The intuitive description of a watershed transform is quite simple: if we consider the image as a topographic relief, where the height of each point is directly related to its gray level, and consider rain gradually falling on the terrain, then the watersheds are the lines that separate the lakes (actually called catchment basins) that form. Generally, the watershed transform is computed on the gradient of the original image, so that the catchment basin boundaries are located at high gradient points. The watershed transform has been widely used in many fields of image processing, including medical image segmentation. Nedzved [8] used morphological operators to segment cells in images with sparse density, Demandolx [9] used a gray level thresholding method to segment subcellular structures in Hela cells and Sjostrom [10] used artificial neural network (ANN) to automatically count cells. Cullen [11] used the blob detector, Proxan, to quantify spatial relationships between heme-rich deposits and capillaries. This tool is designed for separating objects based on color difference between them. It requires an image stained with two different antibodies as an input. For a single labeled image (e.g., a confocal image of retina stained with TO-PRO 3-iodide, a nuclear stain), this method requires that objects in an image are artificially marked with distinct colors. Additionally, there are some commercial software products (Metamorph and Bioquant) that provide object-counting and feature detection. However, these tools often fail to provide reliable results and require intensive user interaction in order to obtain user-given initialization or parameter settings for accurate results. Furthermore, these tools are not designed to analyze immunofluorescent images, which present unique challenges, especially in tissues like the retina where cells are densely packed (600 cells in 512 x 100 pixels). Uneven staining can cause intensity variations within cell layers, and non-uniform DNA distribution inside the nucleus can cause intensity variations within individual cells. There is a need for robust methods for automatically counting nuclei with consistently high accuracy and reliability in large sets of digital micrographs.

In this paper, we present methodology for automatically detecting nuclei, and therefore cell bodies, from a 2-D digital micrograph. The proposed approach provides an accurate, simple, and reliable method to count cells, nuclei, or other objects in sectioned materials. In order to have a scientific basis for selecting optimal parameters of the method, we mainly focus on retinal images, in particular the outer nuclear layer (ONL). Specifically, we detect fluorescent labeled photoreceptor nuclei from confocal images of control and degenerating feline retina as a result of retinal detachment. To show that the proposed method can be applied to many types of images without significant effort, we also tested it with images acquired by transmitted light and epi-fluorescent microscopy, and from tissue in which the contrast of nuclei was low. The proposed nucleus detector has a number of advantages over manual analysis and other currently available or proposed automatic/semi-automatic methods including objectivity, simplicity, and applicability.

Methods

Materials

The basis of our study is a set of immunofluorescent retinal images which have been collected by confocal imaging for understanding the mechanisms underlying the loss and recovery of vision following retinal detachment and reattachment. We collect stacks of serial optical sections (often termed a z-series) from a 100 μm thick retinal tissue section and use only a single optical focal plane image from each z-series to count nuclei within the specific focal plane. We can avoid counting the superimposed nuclei in multiple depth planes by using a single focal plane image instead of a multiple focal plane superimposed image (composite or projection view).

Photoreceptor cells have received the greatest attention in these studies since photoreceptor outer segment degeneration and cell death are considered a major effect of detachment. Previously it has been shown that the number of photoreceptors decrease after detachment [4,12] (Figure 1). Such degeneration of photoreceptors has been measured in various ways in different studies [3,4,13]: (1) the number of rows of nuclei in the ONL, (2) the area of the ONL, (3) the thickness of the ONL, and (4) the number of nuclei in the ONL. The values of these measurements are usually represented as change over time which is then used as an index of photoreceptor degeneration. It has been verified that the ONL appears to be much more loosely packed with nuclei compared to normal as a result of loss of cells following detachment [4,6]. ONL thickness or area, however, may not always give an accurate measure of cell loss. We therefore used these data to compare with results obtained using the newly developed automated nucleus detector.

Nucleus as a blob

Filtering is a very general technique of transforming image gray levels in some way so as to enhance certain features. It has received more attention than any other area of image processing and there are detailed reference works available [14,15]. Template matching is a simple filtering method for detecting a particular feature in an image. If the appearance of this feature in the image is known accurately, one can try to detect it using template matching. The template used in this matching is a subimage that looks just like the image of the object. A similarity measure is computed which reflects how well the image data match the template for each possible location.

Figure 1 shows a confocal image of normal feline retina illustrating the nuclear layers of the retina. In the image, nuclei can be approximated as simple, nearly circular shapes, which we refer to as blobs. Therefore, our study focuses on developing an efficient detection solution for nuclei, a class of blob-like structures as roughly convex local intensity distributions whose iso-level contour is approximately ellipsoidal with some irregularities that do not destroy the ellipsoidal topology. First, we need to model a blob to use as our template for detecting the nuclei in an image.

A single plane image will always show a slice of the individual nuclei. The boundary of each nucleus shows up as strong intensity discontinuities in an image and the intensity distribution of some nuclei are multi-modal because of inconsistent staining and biological characteristics such as the DNA distribution (Figure 2A,B). However, the intensity distribution can be assumed to be uni-modal under the appropriate amount of Gaussian blurring. After Gaussian blurring, the profile of a nucleus becomes a ridge with smooth change of gray level. Therefore, a blob can be modeled as a 3-D surface generated by rotating a ridge profile around its central axis (Figure 2C). If we model the nuclei as this blob with some additive Gaussian noise, we can design an optimum linear blob detector by rotating the second derivative of a Gaussian around its central axis. This 2-D filter is called Laplacian of Gaussian (LoG) [16]. The general idea of the LoG is to detect edges and lines in images by determining the peak point of the ridge as accurately as possible given the ridge profile is corrupted by certain amount of Gaussian noise. LoG has been utilized in the image processing community for detecting edges [14,15]. In our work, we utilize the inverted Laplacian of Gaussian (LoG) as our blob detector. We model the nuclei as circular objects although these objects mostly resemble ellipsoids. Our objective in using a circular model, a very general shape model, is to achieve a rotation invariance in our detection. Otherwise it is possible that we are overfitting our design to the training images.

Nuclei detector design

Once we have a blob detector, the blob centers are detected with the following two steps: 1. Blob detector design. The LoG filter is designed such that the diameter of the filter is proportional to the average diameter of nuclei in the image. For example, the average size of photoreceptor nuclei in the feline retina is 4-6 μm so the diameter of the filter can be set as 5 μm. The filter size in μm can be easily converted to pixel size by using the metadata embedded in a given image. The given retinal image is then filtered by the LoG. This operation results in a smooth continuous image of which the local maxima correspond to blob centers.

Search for local maxima. We search the filtered output for local maxima. The minimum distance between blob centers is used as the search radius for the local maxima, and this parameter is defined to be proportional to the filter size. In summary, the nucleus detector requires two inputs: (1) the cell size in μm or equivalent in pixels, and (2) the minimum distance between cells. The nuclear size to detect in biological tissues is usually well known. A schematic diagram for a nucleus detector is shown in Figure 3.

Evaluation of the nuclei detector

The goal of the nucleus detector is to generate counts of nuclei within the tissue layer of interest that are close to that obtained by manual counting. The manual count value, which is known as ground truth, is compared with the results of the automatic nucleus detector using various combinations of parameters. To estimate optimal parameters of the nucleus detector, we evaluate its performance using error criterion as

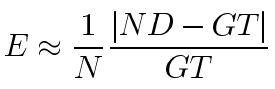
where N is the number of images in the training set, ND and GT is the number of nuclei detected by our nucleus detector and by manual counting, respectively.

Because manual counting is time-consuming, we obtained ground truth for only 41 retinal images and, due to our small data set, we employ the leave-one-out cross-validation method to evaluate the detector's performance. That is, we train the nucleus detector 41 times, each time leaving out one image from the training data set, and using only the omitted image to compute the error. The resulting estimates of generalized error are used for choosing the optimal parameters for the nucleus detector.

The performance of the proposed nucleus detector depends on two factors. First, how well the filter approximates the shape of a nucleus is determined by filter size and standard deviation μ. Second, how well the local maxima are determined which is dependent on the minimum distance between blob centers. Since we search the filter output for local maxima, μ does not affect the performance of the nucleus detector. Thus, we vary two parameters: cell size (cs) in μm and the proportion (p) of the minimum distance between blob centers and filter size (fs), where fs is defined as

where round[x] is the integer closest to x. The parameter cs is varied by five different values from 4 to 8. The range of the values is determined by the cell size within the ONL. The parameter p varies by ten different values from 0.1 to 1. Thus, we have a total 5-10 combinations, and 41 runs are conducted for each combination. We find the nucleus detector achieved a maximum performance (i.e., a minimum error) at cs=5 μm, p=0.5. In practice additional training is not needed, and users simply can apply the optimal parameters to any type of retinal images given that image resolution is known. The summary of test result is shown in Figure 4.

Results

In general, a good nucleus detector should satisfy the following three criteria: (1) accurate so that it can approximate manual counting; (2) simple and computationally efficient; providing reliable results; and (3) applicable to a wide variety of image types with minimal user interaction including parameter settings or preprocessing of the given image. To show that our nucleus detector satisfies these three criteria, we apply it to various sets of retinal images (e.g., confocal images of cat retina and transmitted light microscope images of mouse retina) as well as other images commonly generated by all biologists (e.g., DNA dot blots and fluorescent cell images).

Accuracy

Application to confocal images of the retina. We presented the results of applying the nuclei detector to a series of confocal images of control and detached retinas. Here we focus on detecting nuclei within the outer nuclear layer (ONL) and the inner nuclear layer (INL). 41 digital images of normal and 3-day detached feline retinas (21 control images and 20 3-day detached retinal images) are generated with an Olympus FluoView laser scanning confocal microscope from tissue sections stained with TO-PRO. We use a single optical section image 0.5 μm thick from each z-series so that we can avoid counting superimposed nuclei in multiple planes. For each image, we manually create a mask to define the boundary of the ONL and the INL (Figure 5). The same data set is used for manual counting to create ground truth. Each image is manually counted three times independently to measure intra-observer variation. For the ONL, the average variation over 41 images is 1.8% ranging from 0.2 to 5.35%. On the other hand, the average variation for the INL is higher than that of the ONL as 3.1% ranging from 0.78 to 8.41%. Since the INL consists of three different types of cells that are packed closely together, the boundaries of optically sliced cell bodies within the INL are poorly defined. Those ill defined boundaries results in large variation in manual counting.

We found optimal parameters of the nucleus detector for the ONL (cs=5 μm, p=0.5) through the leave-one-out cross validation. Since we defined the filter size as

the filter size can be computed automatically by using image resolution information extracted from the image. For example, when the image resolution is 0.324 μm per pixel, the filter size is computed as

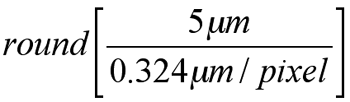
that is, 15 pixels. In other words, the filter size is automatically tuned to the cell size given a retinal image with the image resolution. Then we apply the optimized nucleus detector to the data set. To evaluate the performance of the nucleus detector, the result is compared with the ground truth. The automated nucleus detector approximates the number determined by manual counting. The average absolute error of the nucleus detector is 3.67% ranging from 0 to 6.07% for the ONL. Considering intra-observer variation is 1.8%, the results from our nucleus detector is promising. Even though we do not have a ground truth of (x,y) coordinates of detected nuclei, the locations of detected nuclei overlayed on the image seem visually acceptable (Figure 6A,B). Note that the contrast of the image shown in Figure 6B is not high enough to assure visibility so that variation among the three manual counting results of a given image become relatively high at 3.37%. For the INL, the average absolute error of the nucleus detector is relatively high as 8.52% ranging from 0 to 13.76% for the INL. Large variation in manual counting for the INL results in a large error for the nucleus detector. Thus, we need to develop more elaborate filters to handle tissue with nuclei of multiple sizes and shapes to improve our detection result.

Applying cell counting to retinal detachment. Automated nuclear counts are used to verify the finding that the number of photoreceptors decrease in response to a retinal detachment. In the feline model, retinal detachment leads to the death of some photoreceptor cells [4,6]. Figure 7 shows the average number of photoreceptor nuclei per mm² of retina in control eyes and those with 3-day detached retinas using the manual counting method. The control retinas have, on average, 37503 nuclei/mm². After 3 days of detachment, this number is reduced to an average of 33590 nuclei/mm² (p=0.0001). Even though the average number of photoreceptor nuclei is not exactly the same as the manual count, the nucleus detector captures relative differences in cell density between normal and 3-day detached cases and reaches the same conclusion as manual counting (Figure 7). For the INL, manual counts in 3-day detached retinas would not be considered statistically different from those in normal retinas (p=0.05309; Figure 8). Thus, both manual counting and the nucleus detector result in the same conclusion; the number of cells within the INL does not change in response to 3-day retinal detachment. This is the first time that the number of cells in the INL have been counted verifying an earlier qualitative prediction of cell death in the inner retina in response to retinal detachment [6].

Application to large field of view images. We apply the nucleus detector to a mosaic consisting of eight overlapping images of 3 day detached cat retina. These images are acquired with 5 to 20% overlap in order to align multiple images automatically. The registration technique used is based on the automatic detection of feature points; the estimation of the transformation is obtained using robust estimators on the putative matches obtained matching the intensities of the point neighborhoods [17]. This technique has been widely used to register the remote sensed images. To ensure high quality results containing the maximum amount of original unchanged data blended without blur and abrupt intensity differences, a modern blending technique is used [18]. By using a mosaic, we can count photoreceptor nuclei over a large area of the cat retina without sampling within a tissue. There is a large amount of work to estimate cell numbers from the average cell density of the region in which counting boxes are distributed [1,19,20]. From this work, it has been determined that the larger the tissue and steeper the gradients in cell density, the greater the margin of error. The proposed nucleus detector overcomes these potential errors because no assumptions are made about size, shape or regional difference in cell density. Therefore, it provides not only reliable results with greater confidence but also greater insight into relationships between cells and tissues.

Applicability to varying sample preparation

Application to laser scanning confocal images stained with antibodies. We applied our method to confocal images stained with various antibodies that did not recognize nuclear antigens. Thus, in the images used, the antibodies do not identify the nuclei above background levels. Since confocal retinal images are generated by using fluorescence, only specific regions where fluorescent dye molecules bind are visualized. Therefore, the brightness range within the image is very small. If the antibody does not bind to the ONL, then the ONL usually appears as a dark region where the intensity value of a pixel is close to zero (Figure 9A). The histogram shown next to the image is a plot of number of pixels at each of the 256 possible brightness levels. The narrow peak indicates that only a few of the levels are represented. Since the brightness range within the image is very small, there is not enough contrast to visualize structures within the ONL. Therefore, the visibility of the ONL structures should be improved by stretching contrast so that the values of pixels are reassigned to cover the entire available range, thus making the nuclei visible. We apply a histogram equalization method [15] to the image so that individual nuclei within the ONL can be discriminated (Figure 9B). This histogram plotted with the image in Figure 9B now shows counts of pixels for gray levels that are spread out across the available brightness scale. The results show that the proposed method estimates the location of a cell body even though the antibody used does not recognize and bind to nuclear portions of the cell (Figure 9). In this context, cell counting does not need to be limited to results obtained with nuclear specific stains such as TO-PRO or DAPI. Furthermore, our nucleus detector performs better than manual counting especially where the contrast of the region is low (Figure 9E,F). Since our approach estimates local maxima of the filter output, the nucleus detector still can identify individual nuclei even when the contrast of the region is low or the intensity within the region varies dramatically.

Application to bright-field images of retina. We also apply the nucleus detector to images generated by transmitted light microscopy of normal mouse retina (Figure 10). The filter size is set to 30 pixels and the minimum distance between blob centers is set to 15 pixels (filter size >0.5), which is the same optimal parameter calculated from feline retina. The result shows that the proposed method can approximate the center of a cell quite well under these conditions even without fine tuning of parameters.

Application to other images. We test the proposed method with various images without tuning parameters. Figure 11A shows an image of cultured cells and demonstrates that nuclei can be detected with a single filter even though the size of nuclei within the image are all different. Even though the blob is bigger or smaller than the designed filter, the value of filter output is still the local maximum at the center of the blob. Therefore, searching local maxima of filter output enables detecting various sizes of blobs. Similarly, Figure 11B consists of various shapes and sizes of blobs downloaded from Image J. Some of blobs are multi-lobed and each lobe can be as big as other single-lobed blobs. By applying a single filter with a median size blob within an image, we can detect all blobs successfully. Since the proposed method assumes the blob as a circular object, the filter output will have multiple local maxima within the blob using the filter designed for single-lobed blobs. Such multiple local maxima result in double detected cells. However, they can be easily post-processed by a simple morphological operation. Estimating local maxima can result in detecting some false positive blobs, but they could also be eliminated by tuning the parameters.

Practicality

A number of manual counting methods have been developed. While they are accurate, they are often difficult and tedious to use. The proposed nucleus detector is simple and automated. However, a filter size and the minimum distance between cells must be defined. The default value of the minimum distance can be set as half of the filter size as was shown before and the filter size can be selected roughly from a given sample image. In biological fields, information about cell or nuclear size is usually well known. Therefore, the added effort is not significant.

Discussion

In this paper, we described a nucleus detector that automatically detects the number of nuclei in digital micrographs and can thus be used for counting cells. Initially, we evaluated the performance of the nucleus detector with confocal images of feline retina but found it useful for a wide variety of preparations. For detecting photoreceptor nuclei, the nucleus detector performed very well with an average error of 3.67% ranging from 0 to 6.07%. However, we found that the average error when used to count the INL was relatively high with an average error of 8.55% (ranging from 0 to 13.76%). The INL consists of several different types of cells in which the size and shape of nuclei vary. Therefore, we need to design a more robust filter to detect multiple types of cells with different sized and shaped nuclei. The advantages of the proposed method are its simplicity and reliability to detect any blob-like structures such as nuclei. For example, when using this method to detect nuclei in retinal tissues, no parameters need to be set. Moreover, it is computationally efficient so it is applicable to use across large expanses of tissue eliminating the need for regional sampling which causes the potential errors. It is especially valuable for tissue with steep gradients in cell number (i.e., with distinct layers), such as brain and retina. Additionally, the proposed method can be used on a variety of sample preparations or imaging methods, indicating its widespread applicability.

We use histogram equalization to enhance the visibility of features within an image. The histogram equalization method increases the visual contrast for the pixels present, but it does not increase the ability to discriminate subtle variations in gray scale that are not in the original image. It also magnifies the brightness difference associated with noise in the original image. Therefore, we need to develop a new contrast stretching method so that we can increase the contrast while suppressing the brightness of noise.

Automated measurement from microscopy images is becoming an increasingly important tool in biology. The technique we suggest here, for the automated detecting of nuclei is especially useful on a large scale. Moreover, we can extract additional information based on the nuclei detection results, including thickness of a layer and local cell density within a region (e.g., a specific layer of the retina or brain) [21]. We found that quantitative analysis based on nuclei detection not only corroborated conclusions derived from manual measurements and qualitative assessment, but also provided significant information about local structural changes during retinal detachment. This additional information will help us to determine if there is a correlation between the thickness of the ONL and the density of photoreceptor cells, and whether it is possible to discriminate cones from rods by looking at the pattern of DNA distribution within their nuclei.

The proposed nucleus detector has been implemented as a plug-in for the public domain NIH image processing and analysis program, Image J (version 1.34 developed at the US National Institutes of Health and available). The nucleus detector with sample images and instructions are available at Bio-Image.

Acknowledgements

We wish to acknowledge Camille Cazon for manual counting, Kellen Betts for the sample preparation, Thomas Kuo for developing the ImageJ plug-in and Dmitry Fedorov for providing the mosaic images. This research is supported by NSF number ITR-0331697 and NIH number EY-00888.

References

1. Williams RW, Rakic P. Three-dimensional counting: an accurate and direct method to estimate numbers of cells in sectioned material. J Comp Neurol 1988; 278:344-52. Erratum in: J Comp Neurol 1989; 281:335.

2. Paskowitz DM, Nune G, Yasumura D, Yang H, Bhisitkul RB, Sharma S, Matthes MT, Zarbin MA, Lavail MM, Duncan JL. BDNF reduces the retinal toxicity of verteporfin photodynamic therapy. Invest Ophthalmol Vis Sci 2004; 45:4190-6.

3. Michon JJ, Li ZL, Shioura N, Anderson RJ, Tso MO. A comparative study of methods of photoreceptor morphometry. Invest Ophthalmol Vis Sci 1991; 32:280-4.

4. Lewis GP, Charteris DG, Sethi CS, Fisher SK. Animal models of retinal detachment and reattachment: identifying cellular events that may affect visual recovery. Eye 2002; 16:375-87.

5. Sakai T, Calderone JB, Lewis GP, Linberg KA, Fisher SK, Jacobs GH. Cone photoreceptor recovery after experimental detachment and reattachment: an immunocytochemical, morphological, and electrophysiological study. Invest Ophthalmol Vis Sci 2003; 44:416-25.

6. Fisher SK, Lewis GP, Linberg KA, Verardo MR. Cellular remodeling in mammalian retina: results from studies of experimental retinal detachment. Prog Retin Eye Res 2005; 24:395-431.

7. Malpica N, de Solorzano CO, Vaquero JJ, Santos A, Vallcorba I, Garcia-Sagredo JM, del Pozo F. Applying watershed algorithms to the segmentation of clustered nuclei. Cytometry 1997; 28:289-97.

8. Nedzved A, Ablameyko S, Pitas I. Morphological segmentation of histology cell images. Proceedings of 15th International Conference on Pattern Recognition, Barcelona, Spain, 3-8 September 2000; 1:500-503.

9. Demandolx D, Davoust J. Multiparameter image cytometry: from confocal micrographs to major subcellular structures in fluorescence microscope images of hela cells. Bioimaging 1997; 5:159-69.

10. Sjostrom PJ, Frydel BR, Wahlberg LU. Artificial neural network-aided image analysis system for cell counting. Cytometry 1999; 36:18-26.

11. Cullen KM, Kocsi Z, Stone J. Pericapillary haem-rich deposits: evidence for microhaemorrhages in aging human cerebral cortex. J Cereb Blood Flow Metab 2005; 25:1656-67.

12. Anderson DH, Stern WH, Fisher SK, Erickson PA, Borgula GA. Retinal detachment in the cat: the pigment epithelial-photoreceptor interface. Invest Ophthalmol Vis Sci 1983; 24:906-26.

13. Li ZY, Tso MO, Wang HM, Organisciak DT. Amelioration of photic injury in rat retina by ascorbic acid: a histopathologic study. Invest Ophthalmol Vis Sci 1985; 26:1589-98.

14. Gonzalez RC, Woods RE. Digital image processing. Reading (MA): Addison-Wesley; 1992.

15. Russ JC. The Image Processing Handbook. 2nd ed. Boca Raton: CRC Press; 1995.

16. Canny JF. Finding edges and lines in images [Master's thesis]. Cambridge: MIT Artificial Intelligence Laboratory; 1983.

17. Kenney CS, Manjunath BS, Zuliani M, Hewer GA, Van Nevel A. A condition number for point matching with application to registration and postregistration error estimation. IEEE Trans Pattern Anal Mach Intell 2003; 25:1437-54.

18. Fedorov D, Fonseca LMG, Kenney C, Manjunath BS. Automatic registration and mosaicking system for remotely sensed imagery. SPIE 9th International Symposium on Remote Sensing; 2002; Crete.

19. Abercrombie M. Estimation of nuclear population from microtome sections. Anat Rec 1946; 94:239-47.

20. Howard V, Reid S, Baddeley A, Boyde A. Unbiased estimation of particle density in the tandem scanning reflected light microscope. J Microsc 1985; 138:203-12.

21. Byun J, Vu N, Sumengen B, Manjunath BS. Quantitative Analysis of Immunofluorescent Retinal Images. IEEE International Symposium on Biomedical Imaging: From Nano to Macro. 2006; Arlington (VA).