Appendix 1. Estimating sensitivity

This appendix explains the method used to assess the resolutions of the fluorophore systems. The data were collected by measuring the fluorescence enhancement of solutions of known concentrations of dsDNA. Linear models of the expected value of Y given X (E(Y|X)) were developed of the form:

The resolution for each method is the smallest difference that can be detected by that method. We chose a statistical criteria for detecting the differences. To do this, we used a balanced design that greatly simplifies the computations. In computations, we also assumed the usual regression assumption of homoscedasticity held, though this was verified after the data were collected. Our approach used the t-test for detecting significant differences. It can be shown that for a two sample t-test [9] with a balanced design and equal variance (s_e²), the test statistic is:

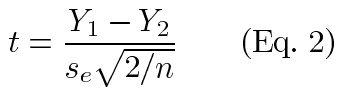
Substituting equation 1 in equation 2 and simplifying, we see that:

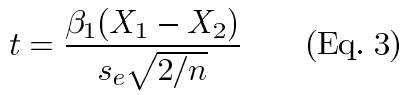
At the point where statistical significance is reached, the test statistic equals the critical value (t_c) and we can solve for resolution (ΔX):

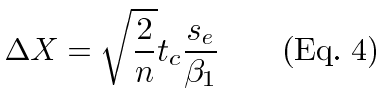
Within an experiment, t_c and n are constant. These are also constant across experiments of identical design. Estimates of the other quantities are easily taken from the output of regression software. The slope of the regression line estimates β₁ and the mean square error estimates s_e² (or root mean square error estimates s_e). This allows us to easily compare the resolutions from identically designed experiments using the relative resolutions (θ):

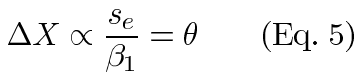
Thus, large values of β₁ give a better resolution, as we would expect. Similarly, the statistical noise seen in a larger variance limits the resolution.