Figure 3. Visual field evaluations with Goldmann perimetry (left column: images of the left eye, right column: images of the right eye).
A: Patient JU#1085 shows preserved peripheral visual fields in the V-4e isopters, although there were constricted visual fields
with central scotoma of the II-4c isopters (23 years of age). B: Patient JU#1303 shows preserved peripheral visual fields in the V-4e isopters, although these were constricted especially
in the superior visual fields of the I-4e isopters (11 years of age).
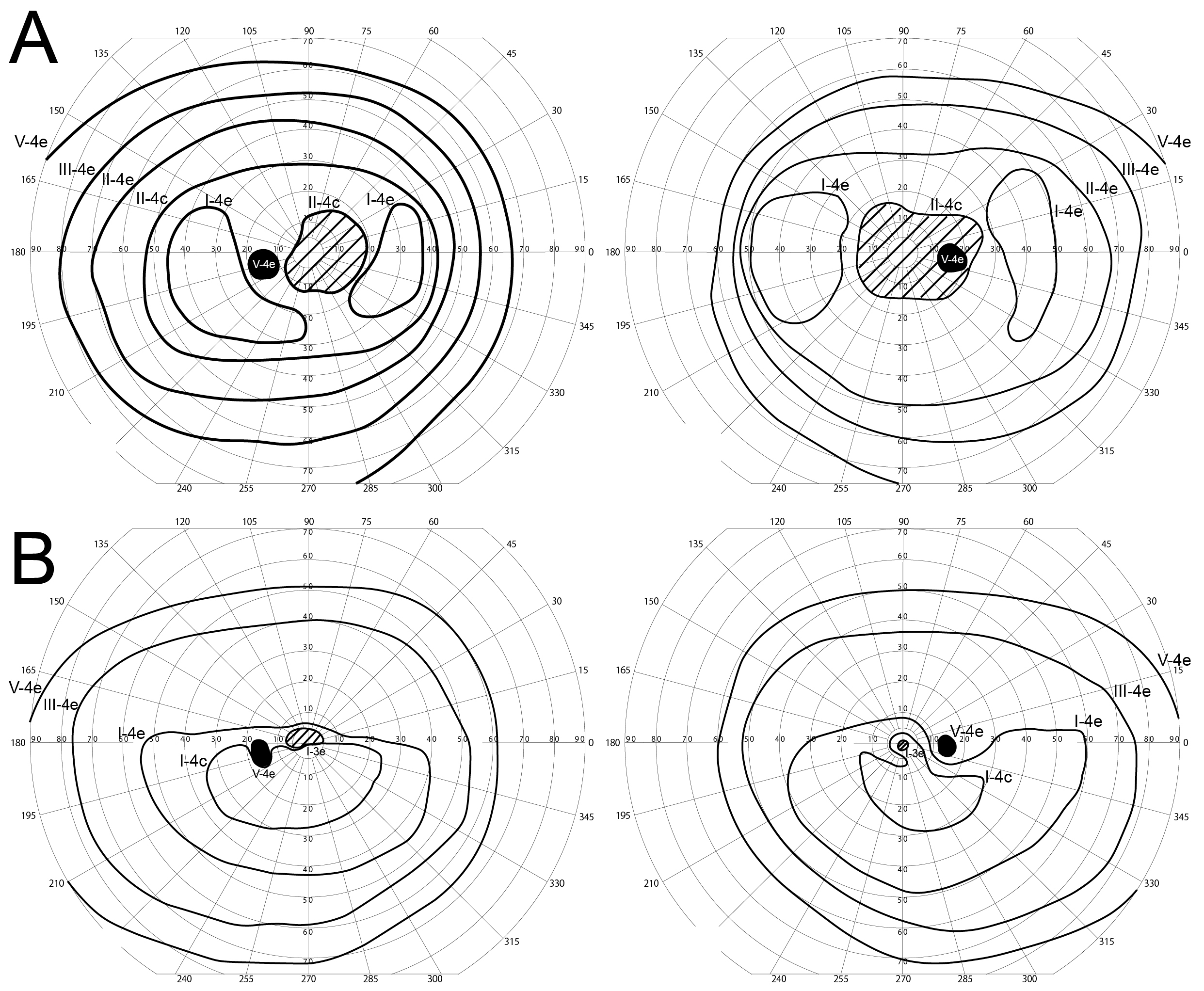
 Figure 3 of
Katagiri, Mol Vis 2018; 24:286-296.
Figure 3 of
Katagiri, Mol Vis 2018; 24:286-296.  Figure 3 of
Katagiri, Mol Vis 2018; 24:286-296.
Figure 3 of
Katagiri, Mol Vis 2018; 24:286-296. 